解答と解説の実況中継【中１数学「図形編①」】

解答と解説の実況中継【中１数学「図形編①」】

解答と解説の実況中継【中１数学「図形編①」】

これは『１０分テスト！中１数学の総復習プリント「図形編①」』の解答と解説です。
インターネットという環境を活かし、かなり見やすく、さらに詳しく、授業の実況中継をするように書いておきました。
（紙のプリント等ではこれは難しいのです）

○か×かだけではなく、途中式や考え方の道筋が正しいかということをしっかり確認するのがレベルアップの秘訣です。
（重要：勉強で一番大切なこととは何か【これを知らずに勉強してはいけない】）

では詳しい解答と解説、行きましょう！

※数式が見られない場合はこちらへ⇒（※画像版）

①の解答と解説

半径が４㎝の円の周の長さと、円の面積をそれぞれ求めよという問題です。
どちらも公式がありますが、覚えていますか？

まずは周の長さからいきましょう。

円周の長さ=直径 × \(\pi\)

これが円周の公式です。
直径 × \(\pi\) なので、２ × 半径 × \(\pi\) と言っても同じです。
それゆえ、半径を\(r\)として、円周の長さの公式を文字式で表すと

円周の長さ＝２\(\pi r\)

となります。

では公式がわかったところで代入していきましょう。
半径は４なので

２×４×\(\pi\) ＝８\(\pi\)

が答えです。

次は円の面積ですね。
公式は

円の面積＝半径 × 半径 × \(\pi\)

です。
こちらも半径を\(r\)として文字式で表すと

円の面積＝\(\pi r^{ 2 }\)

となります。
では公式を確認できたら代入しましょう。

４×４×\(\pi\)＝１６\(\pi\)

となりますね。

よって、円周は \(8 \pi cm\)　円の面積は \(16 \pi cm^{ 2 }\) です！

②の解答と解説

半径１０cm、中心角７２°のおうぎ形の弧の長さと面積をそれぞれ求めなさいという問題です。

おうぎ形の弧や面積についてはさまざまな求め方があり、学校の先生によっても教え方が違います。
塾では生徒の説明を聞き、一人一人のやり方に合わせて教えるのですが、今回は「比」をつかった簡単なやり方にしたいと思います。

どんな比かというと、

円：おうぎ形

という比です。
円は、「おうぎ形をそのまま丸くした円」を使います。

実は、円：おうぎ形では、次の３つの比がすべて同じになります。

①　角度の比　⇒　円の中心角３６０°：おうぎ形の中心角

②　長さの比　⇒　円周の長さ：おうぎ形の弧の長さ

②　面積の比　⇒　円の面積：おうぎ形の面積

この３つ。
この３つがすべて同じ比になるので、問題からわかる部分を当てはめていって、ヒントの多い所で比例式を作るというやり方をします。

さて、では実際の問題に移りましょう。

まずはフリーハンドで図をかいて、情報を視覚的に整理します。
角度や長さは大体でOKです（下の図も正確ではありません。~~あえて、ですよ？~~）。

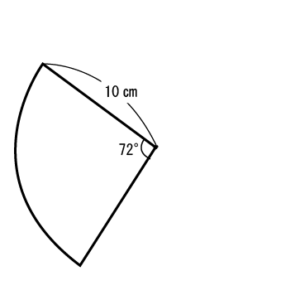
こんな感じですね。
おうぎ形の場合は、ここからさらに「おうぎ形が円だったら」という部分を点線で追加してチェックしておきます。
先ほど説明した「円：おうぎ形」という比を使うためです。

円周の長さは、２×１０×\(\pi\) で２０\(\pi\) です。
また円であれば中心の角度は360°ですね。
ということで下のようになります。

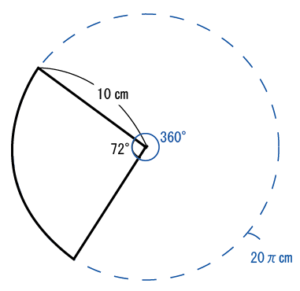
ここまで整理した図から、わかる部分で比を作っていきましょう。

まずは、おうぎ形の弧について考えてみます。
求めたい弧の長さを \(x\) とすると、長さの比が作れますね。

円：おうぎ形＝２０\(\pi：x\)

となります。

後は、角度の比が作れますね。

円：おうぎ形＝３６０°：７２°　です。

この長さの比と角度の比が同じなので、イコールで結んで比例式を解きましょう。
比例式は、外側同士をかけ算したものと、内側同士をかけ算したものをイコールで結んで方程式にして解くんでしたね。

\begin{eqnarray}
20\pi:x&=&360:72 \\
x \times 360&=&20\pi \times 72\\
360x&=&20\pi \times 72 \\
360x \div 360&=&20\pi \times 72 \div 360 \\
x&=&\frac{20\pi \times 72}{360} \\
x&=&4\pi
\end{eqnarray}

よって、弧の長さは \(4 \pi cm\)　となります。

※式の途中のこの部分⇒　\(20\pi \times 72 \div 360\)　の計算、気づきましたか？
あえて \(20\pi \times 72 \) を計算せず、360と併せて約分をしています。
詳しく書くと

\begin{eqnarray}
x&=&\frac{20\pi \times 72}{360} \\
x&=&\frac{2\pi \times 72}{36} \\
x&=&\frac{2\pi \times 2}{1} \\
x&=&4\pi
\end{eqnarray}

こんな感じです。
２０と３６０を÷１０で約分し、その後７２と３６を÷３６して約分しています。

このようにすることで、筆算でのわり算やかけ算をせず、大きい数も扱わずに計算できる場合がたくさんあります。
ミスを減らす効果もあるので、できるだけ取り入れてみましょう。

では、次は面積ですね。

おうぎ形の面積を \(y\)として考えてみましょう。
円の面積は、１０×１０×\(\pi\)＝１００\(\pi\)　となります。
よって面積の比は

円：おうぎ形＝１００\(\pi：y\)　ですね。

これと角度の比３６０°：７２° を組み合わせて比例式を作り、解きましょう。

\begin{eqnarray}
100\pi:y&=&360:72 \\
y \times 360&=&100\pi \times 72\\
360y&=&100\pi \times 72 \\
360y \div 360&=&100\pi \times 72 \div 360 \\
y&=&\frac{100\pi \times 72}{360} \\
y&=&20\pi
\end{eqnarray}

よって、おうぎ形の面積は \(20 \pi cm^{ 2 }\) となります。
※こちらもさっきと同じ計算の工夫がありますね。見つけてみましょう。

ということで、おうぎ形の弧は \(4 \pi cm\)　面積は \(20 \pi cm^{ 2 }\) です！