解答と解説の実況中継【中1数学「図形編②」】
これは『10分テスト!中1数学の総復習プリント「図形編②」』の解答と解説です。
インターネットという環境を活かし、かなり見やすく、さらに詳しく、授業の実況中継をするように書いておきました。
(紙のプリント等ではこれは難しいのです)
○か×かだけではなく、途中式や考え方の道筋が正しいかということをしっかり確認するのがレベルアップの秘訣です。
(重要:勉強で一番大切なこととは何か【これを知らずに勉強してはいけない】)
では詳しい解答と解説、行きましょう!
※数式が見られない場合はこちらへ⇒(※画像版)
①の解答と解説
円錐の表面積を求める問題ですね。
前回のおうぎ形の時と同じく、情報を視覚的に整理するためにフリーハンドで展開図をかきましょう。(長さや角度は大体でOK)
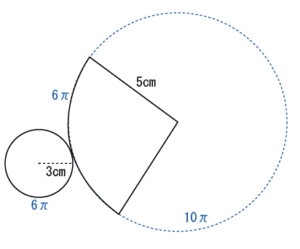
このようになります。
側面積の部分は展開図にするとおうぎ形になるのですね。
おうぎ形の面積を求めることになるので、前回と同じくおうぎ形をそのまま円にした場合の点線もかいておきましょう。
そして長さを書き込んでいきます。
底面の円の半径は3㎝、おうぎ形の辺(半径)は5㎝です。
ちなみに、立体のときにあった高さの4cmは、展開図にすると存在しなくなりますので注意してくださいね。
おうぎ形の弧は底面の円の円周と同じです。
円周は 直径 × \(\pi\) なので、底面の円周は 6\(\pi\) になります。
よっておうぎ形の弧も6\(\pi\) です。
さらにおうぎ形をそのまま円にした場合の円の円周は 10\(\pi\) ですのでこちらも書いておきましょう。
さて、ここまで情報が出そろったら、どんどん面積を求めていきましょう。
まず、底面の円の面積を求めてしまいます。
円の面積=半径 × 半径 × \(\pi\)
(円の面積=\(\pi r^{ 2 }\) )
なので、代入すると
3×3×\(\pi\)=9\(\pi\) ですね。
おうぎ形の方は、前回と同じく「比」をつかったやり方で解いてみます。
どんな比かというと、
円:おうぎ形
という比を利用するのでしたね。
※円は、「おうぎ形をそのまま丸くした円」を使います。
円:おうぎ形では、次の3つの比がすべて同じになります。
① 角度の比 ⇒ 円の中心角360°:おうぎ形の中心角
② 長さの比 ⇒ 円周の長さ:おうぎ形の弧の長さ
② 面積の比 ⇒ 円の面積:おうぎ形の面積
この3つ。
この3つがすべて同じ比になるので、問題からわかる部分を当てはめていって、ヒントの多い所で比例式を作るというやり方をすると前回説明しました。
さて、では円:おうぎ形の比を作っていきます。
長さがわかっているので長さの比はそのまま 10\(\pi\) : 6\(\pi\) でOKです。
面積の比は、円の方は 5×5×\(\pi\)で25\(\pi\) なので、おうぎ形の面積を\(x\)とすると
25\(\pi\):\(x\) となります。
長さの比と面積の比は等しいので、イコールで結んで解きましょう
\begin{eqnarray}
10\pi:6\pi&=&25\pi:x \\
10\pi \times x&=&6\pi \times 25\pi \\
10\pi x&=&6\pi \times 25\pi \\
10\pi x \div 10\pi&=&6\pi \times 25\pi \div 10\pi \\
x&=&\frac{6\pi \times 25\pi}{10\pi} \\
x&=&15\pi
\end{eqnarray}
よって、おうぎ形の面積は \(15 \pi \) となります。
底面の円の面積と側面のおうぎ形の面積を合わせて
\(9 \pi +15 \pi =24 \pi \)
よってこの円錐の表面積は
\(24 \pi cm^{ 2 }\) です!
※式の途中のこの部分⇒ \(6\pi \times 25\pi \div 10\pi \) の計算はちょっとした工夫です。
あえて \(6\pi \times 25\pi \) を計算せず、\(10\pi \)とあわせて約分をしています。
詳しく書くと
\begin{eqnarray}
x&=&\frac{6\pi \times 25\pi}{10\pi} \\
x&=&\frac{3 \times 25\pi}{5} \\
x&=&\frac{3 \times 5\pi}{1} \\
x&=&15\pi
\end{eqnarray}
としています。
\(6\pi \)と\(10\pi \)を÷\(2\pi \)で約分し、その後\(25\pi \)と\(5 \)を÷\(5 \)して約分しています。
このようにすることで、筆算でのわり算やかけ算をせず、大きい数も扱わずに計算できる場合がたくさんあります。
ミスを減らす効果もあるので、できるだけ取り入れてみましょう。
②の解答と解説
こちらは円柱の表面積を求める問題ですね。
早速展開図を大体で書きましょう。
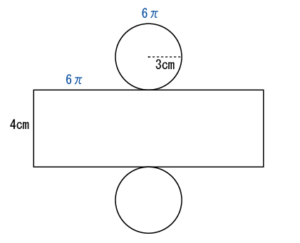
円が二つと長方形が一つという形になりました。
長さも書き込んでいきます。
円の半径、長方形の縦の長さはそのまま書けますね。
長方形の横の長さは、底面の円の周りの長さと同じです。
円周は 直径 × \(\pi\) なので、底面の円周は 6\(\pi\) になります。
よって長方形の横の長さも6\(\pi\) となります。
では、面積を求めていきましょう。
それぞれの円の面積は、3×3×\(\pi\)=9\(\pi\) となります。
長方形は、4×6\(\pi\)=24\(\pi\) ですね。
後は、円2つと長方形1つの面積を合わせて完成です。
9\(\pi\)×2+24\(\pi\)=42\(\pi\)
ということで、円柱の表面積は \(42 \pi cm^{ 2 }\) です!
終わりに
10分テスト!中1数学の総復習プリント「図形編②」(問題)はどうでしたか?
円錐の表面積は頻出ですが、間違う人が多いので気をつけましょう。
前回解説したおうぎ形を比で求めるやり方がわかると、とてもやりやすくなると思います。
繰り返し練習しましょうね!
※前回のおうぎ形の問題⇒10分テスト!中1数学の総復習プリント「図形編①」(問題)


