解答と解説の実況中継【中1数学「関数編①」】
これは『10分テスト!中1数学の総復習プリント「関数編①」』の解答と解説です。
インターネットという環境を活かし、かなり見やすく、さらに詳しく、授業の実況中継をするように書いておきました。
(紙のプリント等ではこれは難しいのです)
○か×かだけではなく、途中式や考え方の道筋が正しいかということをしっかり確認するのがレベルアップの秘訣です。
(重要:勉強で一番大切なこととは何か【これを知らずに勉強してはいけない】)
では詳しい解答と解説、行きましょう!
※数式が見られない場合はこちらへ⇒(※画像版)
(1)について
①の解答と解説
「yがxに比例し」と書いてありますね。
比例ときたら、
\begin{eqnarray}
y=ax
\end{eqnarray}
です。
これが比例の基本の式なので、比例と言われたら最初にこれを思い浮かべましょう。
そして大体でいいのでグラフも同時に思い浮かべます。下のような原点を通る直線です。
(比例のグラフの例)
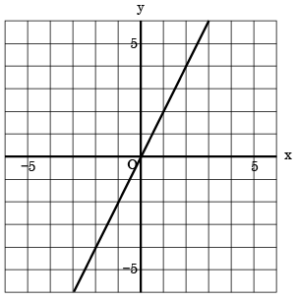
「y=ax」のaの部分は比例定数といいますが、難しい話は置いておきます。
比例におけるこのaが表すのは、「どのくらい線が傾くか」ということです。
原点などから右に1進んだとき、上下にどのくらい進むのか、という傾きです。
式を求めなさいと言われたら、このaを求めることだと思っていいでしょう。
また、xとyは座標の組み合わせを表します。
もしも問題に座標についてのヒントがあったら、その座標を式に代入すると道が開けます。
大体は。
さて、今回は「x=12のとき、y=4である」と問題にありますので、座標のヒントが出ています。
ね?代入です。
「y=ax」という比例の基本の式のxとyに代入すると、
\begin{eqnarray}
4&=&12a \\
12a&=&4 \\
a&=&\frac{4}{12} \\
a&=&\frac{1}{3}
\end{eqnarray}
となります。
よって、答えは
\begin{eqnarray}
y=\frac{1}{3}x
\end{eqnarray}
ですね。ここまできて完成なので、「a=○○」で終わらないように気をつけましょう。
②の解答と解説
「x=-3のとき」とあります。
比例ではxは座標のことなので、やはり代入です。先ほど出した
\begin{eqnarray}
y=\frac{1}{3}x
\end{eqnarray}
の式に代入しましょう。
\begin{eqnarray}
y&=&\frac{1}{3}x \\
y&=&\frac{1}{3} \times (-3) \\
y&=&-1
\end{eqnarray}
これで完成です!
(2)について
①の解答と解説
「yがxに反比例し」と書いてありますね。
反比例ときたら、
\begin{eqnarray}
y=\frac{a}{x}
\end{eqnarray}です。
これが反比例の基本の式なので、反比例と言われたら最初にこれを思い浮かべましょう。
そして大体でいいのでグラフも同時に思い浮かべます。下のような原点を通らない双曲線です。
(反比例のグラフの例)
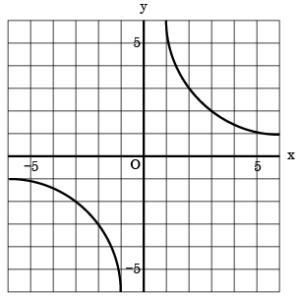
比例と同じく、式を求めなさいと言われたら、このaを求めることだと思っていいでしょう。
また、xとyも比例と同じく座標の組み合わせを表します。
問題に座標についてのヒントがあったら、その座標を式に代入するんでしたね。
今回は「x=4のとき、y=-2である」と問題にありますので、その座標を代入します。
\begin{eqnarray}
y&=&\frac{a}{x} \\
-2&=&\frac{a}{4} \\
\frac{a}{4}&=&-2 \\
\frac{a}{4} \times 4&=&-2 \times 4 \\
a&=&-8
\end{eqnarray}
よって答えは
\begin{eqnarray}
y=-\frac{8}{x}
\end{eqnarray}
です!
②の解答と解説
「y=-8のとき」とあります。
比例ではyは座標のことなので、やはり代入です。先ほど出した
\begin{eqnarray}
y=-\frac{8}{x}
\end{eqnarray}
に代入しましょう。
\begin{eqnarray}
y&=&-\frac{8}{x} \\
-8&=&-\frac{8}{x} \\
-8 \times x&=&-\frac{8}{x} \times x \\
-8x&=&-8 \\
-8x \times -\frac{1}{8} &=&-8 \times -\frac{1}{8}\\
x&=&1
\end{eqnarray}
これで完成です!
※途中式はかなり詳しく書いているので、それぞれの好みで省いてかまいません。
終わりに
10分テスト!中1数学の総復習プリント「関数編①」(問題)はどうでしたか?
簡単に感じた人も油断することなく、繰り返し練習しておきましょう!
ちなみに、繰り返し学習をするときは、間違った問題だけでなく、正解したものも含めてテストすることがレベルアップの近道です。



