小学6年生 立体の体積 問題プリント【まとめテスト】

「小学6年生立体の体積問題プリント【まとめテスト】」の解答と解説です。
（↑クリックすると問題に戻ります）」

解説と解答｜立体の体積の問題プリント【まとめテスト】
まとめ

解説と解答｜立体の体積の問題プリント【まとめテスト】

『小学6年生立体の体積問題プリント【まとめテスト】』について、詳しく解説をしていきます。

○×をつけるだけで終わらせず、自分で説明できるか確認し、くり返しテストしてくださいね。
※くり返しの重要性⇒正解した問題も繰り返した方がいい？【記憶法に関する驚きの実験結果】

1-①の解説と解答

下のような立体（三角柱）の体積を求める問題です。

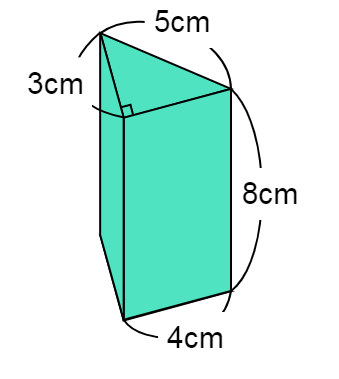
立体の体積を求める公式を利用して計算しましょう。

立体の体積＝底面積 × 高さ

今回は、底面積が三角形ですね。
三角形の面積の公式を使って求めます。

三角形の面積＝底辺×高さ÷\(2\)

以下のような計算になります。

\begin{eqnarray}
4 \times 3 \div 2=6
\end{eqnarray}

底面積がわかったら、後は「高さ」をかけるだけです。

以下のような計算になります。

\begin{eqnarray}
6 \times 8 =48
\end{eqnarray}

よって、答えとなる立体の体積は、

\(48 \) cm³

となります。

図形にはななめの線の長さ\(5\)cmも書いてありますが、三角形の高さは底辺と直角に交わっている線を使います。
数が書いてあると「何とかその数を使いたくなってしまう」人が多いので、注意しましょう。

1-②の解説と解答

下のような立体（横になった三角柱）の体積を求める問題です。

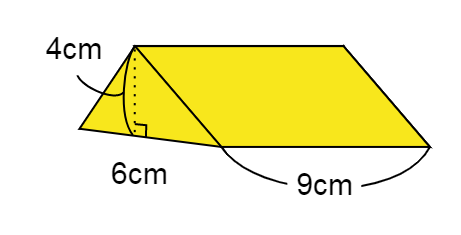
こちらも立体の体積を求める公式を利用して計算しましょう。

立体の体積＝底面積 × 高さ

今回も、底面積が三角形ですね。
三角形の面積の公式を使って求めます。

三角形の面積＝底辺×高さ÷\(2\)

以下のような計算になります。

\begin{eqnarray}
6 \times 4 \div 2=12
\end{eqnarray}

底面積がわかったら、後は「高さ」をかけるだけです。

以下のような計算になります。

\begin{eqnarray}
12 \times 9 =108
\end{eqnarray}

よって、答えとなる立体の体積は、

\(108 \) cm³

となります。

1-③の解説と解答

下のような立体（底面が台形の角柱）の体積を求める問題です。

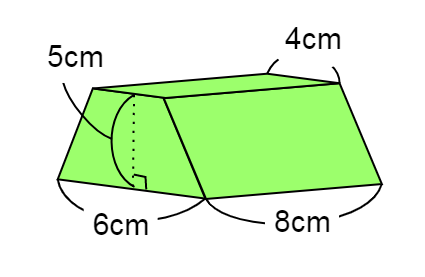
底面積が台形ですね。
台形の面積の公式を使って求めます。

台形の面積＝（上底+下底）×高さ÷\(2\)

以下のような計算になります。

\begin{eqnarray}
(4+6) \times 5 \div 2=25
\end{eqnarray}

底面積がわかったら、後は「高さ」をかけるだけですね。

以下のような計算になります。

\begin{eqnarray}
25 \times 8 =200
\end{eqnarray}

よって、答えとなる立体の体積は、

\(200 \) cm³

となります。

1-④の解説と解答

下のような立体（底面が円の円柱）の体積を求める問題です。

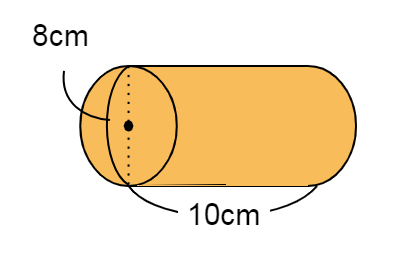
底面が円ですね。
円の面積の公式を使って求めます。

円の面積＝半径 × 半径 × \(3.14\)

図では直径が書いてありますので、まずは半分にして半径の長さを求めます。

\begin{eqnarray}
8 \div 2 =4
\end{eqnarray}

この半径の長さを、円の面積の公式に当てはめていきましょう。
以下のような計算になります。

\begin{eqnarray}
4 \times 4 \times 3.14=50.24
\end{eqnarray}

底面積がわかったら、後は「高さ」をかけるだけですね。

以下のような計算になります。

\begin{eqnarray}
50.24 \times 10 =502.4
\end{eqnarray}

よって、答えとなる立体の体積は、

\(502.4 \) cm³

となります。

2 の解説と解答

下のような図形の体積を求める問題です。
底面の形が台形の角柱と、円柱を半分にしたものを組み合わせています。

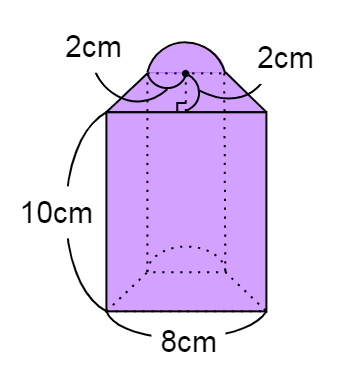
一見すると複雑で難しそうに見えますが、切り分けて簡単に考えましょう。

今回は底面が台形の部分と半円の部分に切り分けます。

まずは底面が台形の角柱から求めていきます。

台形の面積の公式を確認しましょう。

台形の面積＝（上底+下底）×高さ÷\(2\)

公式が確認できたら数を当てはめます。
「上底」は円の直径と重なっているので、\(4\)cmですね。

下のような計算になります。

\begin{eqnarray}
(4+8) \times 2 \div 2=12
\end{eqnarray}

底面積がわかったら、後は「高さ」をかけるだけです。

以下のような計算になります。

\begin{eqnarray}
12 \times 10 =120
\end{eqnarray}

よって、底面が台形になっている部分の体積は、\(120 \) cm³となります。

次は底面が半円になっている部分を求めます。

まずは公式を利用して円の面積を求めてから、それを半分にしましょう。

円の面積＝半径 × 半径 × \(3.14\)

半径が \(2\) cm の円の面積なので、以下のような計算になります。

\begin{eqnarray}
2 \times 2 \times 3.14=12.56
\end{eqnarray}

円の面積がわかったら半分にします。

\begin{eqnarray}
12.56 \div 2=6.28
\end{eqnarray}

底面積がわかったら、後は「高さ」をかけるだけですね。
以下のような計算になります。

\begin{eqnarray}
6.28 \times 10 =62.8
\end{eqnarray}

よって、底面が半円になっている部分の立体の体積は、\(62.8 \) cm³となります。

後は、それぞれの体積をたしましょう。

\begin{eqnarray}
120+62.8=182.8
\end{eqnarray}

よって、答えとなる立体の体積は、

\(182.8 \) cm³

となります！

半円と台形のそれぞれの底面積をたしてから、高さをかけてもOKです。

3 の解説と解答

下の図のような厚さ \(2\) cmのガラスでできた水そうがあります。
この水そうに \(1000\) cm³の水を入れると、水の深さは何cmになるのか求める問題ですね。

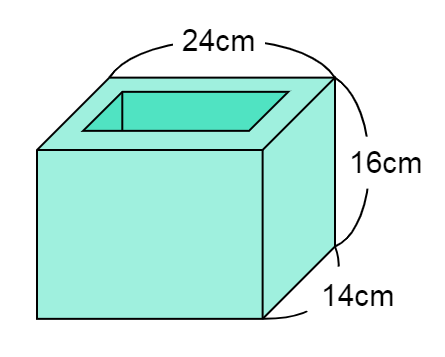
水を入れた後、水がどのような形になっているかを考えてみましょう。
水は水そうに合わせて、直方体になっているはずですね。

その直方体の底面積は、水そうのガラスの厚さ\(2\) cmを引いて考えると、たてが\(10\) cm、横が\(20\) cmになります。

ということは、底面積は以下のような計算で求められますね。

\begin{eqnarray}
10 \times 20 =200
\end{eqnarray}

水の直方体の深さはわからないのですが、水の体積は \(1000\) cm³なので、次のような式が成り立ちます。

\(200\) × 深さ \(=1000 \)

ここから深さを求めるには、\(200\) にかけ算をして\(1000\) になる数をみつけるので、逆に\(1000\) を\(200\) でわり算すればOKです。

\begin{eqnarray}
1000 \div 200 =5
\end{eqnarray}

よって、答えとなる水の深さは

\(5 \) cm

となります！

まとめ

『小学6年生立体の体積問題プリント【まとめテスト】』はいかがでしたか？
立体の体積の問題をマスターするために、

立体の体積の公式を使う
⇒「底面積×高さ」
複雑な図形は、求めやすいように分けて考える

ということを意識して、これからも練習を重ねましょう。

理解した後は繰り返し練習し、立体の体積の単元を得意分野にしてくださいね！
※得意を増やす意味⇒得意を伸ばすか、苦手を克服するかどっちがいい？どちらを優先？

その他の問題に取り組みたい方は⇒『小学生算数プリント一覧』へ