「展開図と見取り図の問題プリント|直方体と立方体①(←クリックすると問題に戻ります)」の解答と解説です。
解答と解説|展開図と見取り図の問題プリント|直方体と立方体①
では、詳しく解説をしていきます。
○×をつけるだけで終わらせず、自分で説明できるか確認し、繰り返しテストしてくださいね。
※繰り返しの重要性⇒正解した問題も繰り返した方がいい?【記憶法に関する驚きの実験結果】
①の解説と解答
まず最初に、さいころを組み立ててしまいましょう。
下の2つの法則を使って頂点が重なる場所をチェックすると、組み立て方が考えやすくなりますよ。
- 展開図で90度になっている辺の頂点どうしと、そのとなりの頂点どうしは重なる
- 展開図で1つとばしの面どうしは、見取り図では平行になる
1つ目の法則で重なる頂点を実際に結んでみるとこのようになります。
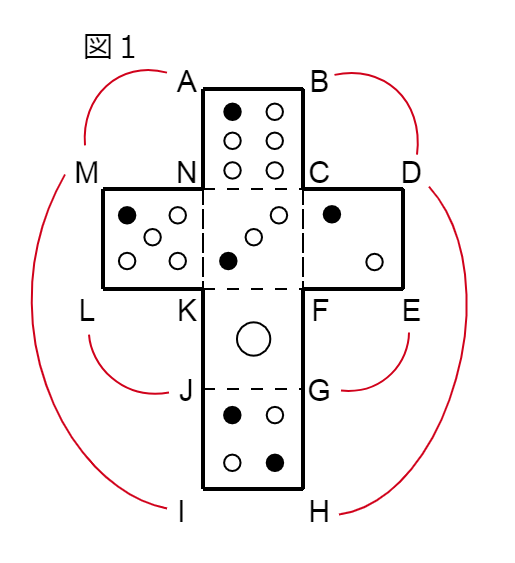
また、2つ目の法則で平行になる面どうしを色分けすると下のようになります。
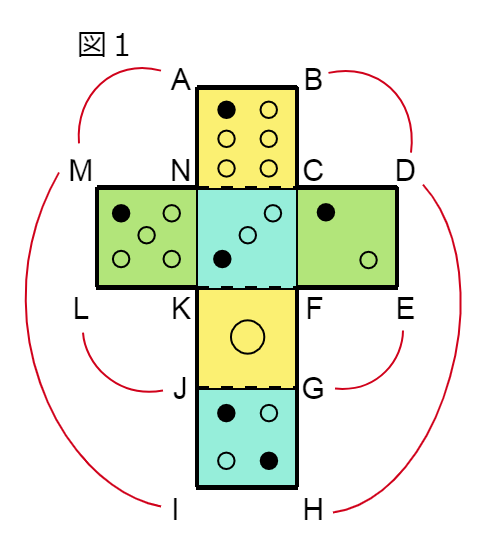
これでかなり組み立てやすくなったかなと思います(難しいなりに)。
では、①の問題は辺DEと重なる辺を答える問題なので、辺DEから組み立ててみましょう。
※厚紙にさいころの目を書いただけなので、さいころの目が表にくるように組み立てましょうね。
奥に向かって折っていくと、赤線で対応させた通り、頂点DとB、頂点EとGがまず重なります。
そして、4の目の面をぱたっと折ると、頂点HがDに重なります。
そうすると辺HGがぴたっと辺DEに重なりますね。
よって、①の答えは、辺HG です。
(1つ目の法則を使うと、組み立てなくても重なる辺はわかったりします)
②の解説と解答
頂点Mと重なる頂点をすべて答えなさいという問題です。
これは、赤線で対応させたものを答えればできてしまいます。
(組み立てなくてもできますが、法則をヒントにしつつできるだけ頭の中で組み立てましょうね。組み立てる能力も伸ばしましょう。)
答えは、頂点Aと頂点I です。
③の解説と解答
1の目の面と平行な面の目の数を答える問題です。
これは、色分けしたものを見ればわかります。
答えは、6 です。
④の解説と解答
5の目の面と垂直な面の目の数をすべて答える問題です。
これは法則をヒントに組み立てて考えましょう。
答えは、1,3,4,6 です。
⑤の解説と解答
辺ABと垂直な面の目の数をすべて答える問題です。
これも法則をヒントに組み立てて考えましょう。
答えは、2と5 です。
⑥の解説と解答
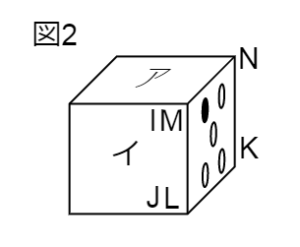
組み立てたさいころを下の図2のように置いたとき、面アの目の数を答えるという問題です。
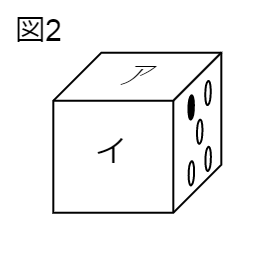
難しくなってきましたね。
これは、ただ組み立てるだけでは考えにくいかもしれません。
ヒントになっている5の目の面について、頂点のアルファベットをチェックしましょう。
下のようになります。
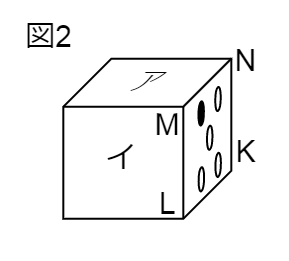
こうしてみると、アの面は辺MNと重なる辺をもつ面であることがわかります。
赤線で対応させた図から、辺MNと重なるのは辺ANです。
辺ANのある面の目の数を答えるので、
答えは、6 です。
⑦の解説と解答
図2の面イの目の並び方を、○と●を使ってかくという問題です。
かなり難しく感じるかもしれませんね。
さきほどチェックしたように、5の目の面の頂点のアルファベットは下のようになります。

イの面は、辺MLと重なる辺をもつ面ですね。
赤線で対応させた図から、頂点MとI、頂点LとJが重なります。
よって、辺MLと重なるのは辺IJです。
書き加えると下のようになります。
ということで、辺IJが右はしに来るようにさいころの目をかけば正解です。
答えは
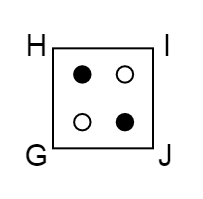
となります!(アルファベットは書かなくてOKです)
まとめ
サイコロの展開図と見取り図の問題プリントはいかがでしたか?
展開図と見取り図をマスターするために、
という法則を使って、これからも練習を重ねてください。
理解した後は繰り返し練習し、展開図と見取り図を得意分野にしていきましょう!
※得意を増やす意味⇒得意を伸ばすか、苦手を克服するかどっちがいい?どちらを優先?
その他の問題に取り組みたい方は⇒『小学生 算数プリント一覧』へ


