「文字と式 問題プリント【まとめテスト②】」の解答と解説です。
(↑クリックすると問題に戻ります)」
解説と解答|文字と式 問題プリント【まとめテスト②】
1 -①の解説と解答
150円のペットボトルを \(x \) 本買う状況で、代金を \(y \) 円として、\(x \) と \(y \) の関係を式に表す問題です。
数量の関係を、まずは「言葉の式」に直して考える
ことが大切です。
「ペットボトルの値段」×「買う本数」=「代金」
となります。
これを文字や数に置きかえていきましょう。
なので、さきほど作った言葉の式をそれぞれの文字と数で置きかえましょう。
答えは、\(150 \times x =y \) となります。
1 -② の解説と解答
①で出した \(150 \times x =y \) の式で、\(x \) の値を 3 としたとき、対応する \(y \) の値を求める問題です。
\(x \) の値を「~」とするとあったら、\(x \) を「~」にかえてみましょう。
今回は \(x \) の値が 3 なので、\(x \) を 3 にかえましょう。
すると、\(150 \times 3 =y \) となります。
\(150 \times 3 \) を計算すれば \(y \) が出るということですね。
よって答えは、\(y=450 \) となります。
1 -③ の解説と解答
①で出した \(150 \times x =y \) の式で、\(y \) の値が 750 となる \(x \) の値を求める問題です。
\(y \) の値が「~」となるとあったら、\(y \) を「~」にかえてみましょう。
今回は \(y \) の値が 750 なので、\(y \) を 750 にかえましょう。
すると、\(150 \times x =750 \) となります。
\(150 \times x =750 \) ということは、
\(750 \div 150 \) をすれば \(x \) がでますね。
よって答えは、\(x=5 \) となります。
2 の解説と解答
\(20-x \times 4 \) の式で表されるものを、ア~エから選ぶ問題です。
※すべてと書いてあるので、一つとは限りません(一つのこともあります)。
こういった問題は、
ことが大切です。
※式にならない場合もあります(それは正解にはなりません)
では、それぞれ文字を使った式にかえていきましょう。
「ア」の文字を使った式
まずは「ア」の
から式にしてみます。
「全部の個数」-「配った個数」=「残りの個数」
なので、\(20-x \times 4= \)残りの個数 となります。
「ア」は正解ですね!
「イ」の文字を使った式
では「イ」にいきましょう。
ですね。
「箱の代金」+「お菓子の代金」=「合計金額」
なので、\(20+x \times 4= \)合計金額 となります。
式が違うので「イ」は違います。
「ウ」の文字を使った式
「ウ」についても確認しましょう。
です。
一人分の枚数は \(x \) 枚なので、これは式になりません。
( \(x= \)一人分の枚数 という式になるとも言えます)
よって「ウ」も違いますね。
(残りの枚数を求める式だったら正解でした)
「エ」の文字を使った式
「エ」についても確認しましょう。
です。
「全部の枚数」-「食べた枚数」=「余った枚数」
なので、\(20-x \times 4= \)余った枚数 となります。
「エ」も正解ですね!
よって答えは、ア と エ です。
3 -①の解説と解答
下の図のような、底辺が \(a \) cm、高さが 8cmの三角形の面積を求めるとき、①~③の式は、ア~ウのどの図から考えたものか答える問題です。
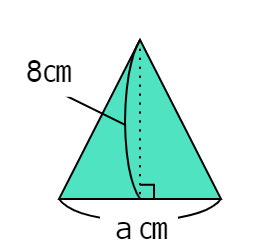
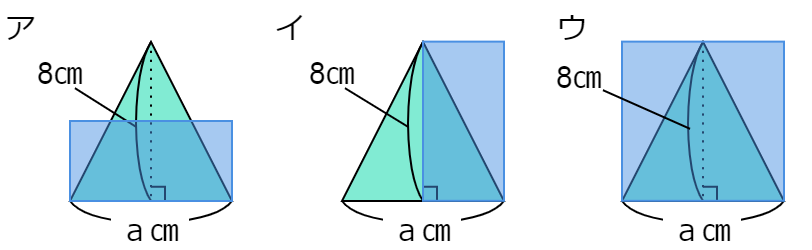
①は \((a \times 8) \div 2 \) という式です。
「かっこ」を先に計算するという約束があるので、この式では \((a \times 8) \) を最初に計算します。
\((a \times 8) \) は「底辺」×「高さ」になっているので、まずは底辺を高さの分だけ広げた面積が出ます。
その計算が表現されている図は「ウ」ですね。

この次に2でわれば、三角形の面積となります。
よって①の答えは、ウ です。
3 -②の解説と解答
\(a \times (8 \div 2) \) という式が、ア~ウのどの図から考えたものか答える問題です。
「かっこ」を先に計算するという約束があるので、この式では \( (8 \div 2) \) を最初に計算します。
\( (8 \div 2)\) は「高さ」÷2になっているので、高さを半分にして、その後で底辺をかけて長方形の面積を求めるというやり方になっています。
その計算が表現されている図は「ア」ですね。
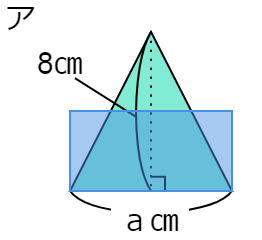
よって②の答えは、ア です。
3 -③の解説と解答
\((a \div 2) \times 8 \) という式が、ア~ウのどの図から考えたものか答える問題です。
「かっこ」を先に計算するという約束があるので、この式では \( (a \div 2) \) を最初に計算します。
\((a \div 2)\) は「底辺」÷2になっているので、底辺を半分にして、その後で高さをかけて長方形の面積を求めるというやり方になっています。
その計算が表現されている図は「イ」ですね。
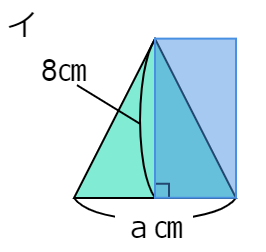
よって③の答えは、イ です。
まとめ
『文字と式 問題プリント【まとめテスト②】』はいかがでしたか?
文字と式の問題をマスターするために、
ということを意識して、これからも練習を重ねましょう。
理解した後は繰り返し練習し、文字と式の問題を得意分野にしてくださいね!
※得意を増やす意味⇒得意を伸ばすか、苦手を克服するかどっちがいい?どちらを優先?
その他の問題に取り組みたい方は⇒『小学生 算数プリント一覧』へ



