「小学6年生 図形の拡大と縮小 問題プリント【まとめテスト】」の解答と解説です。
(↑クリックすると問題に戻ります)
解答と解説|小学6年生 図形の拡大と縮小 問題プリント【まとめテスト】
では、図形の拡大と縮小の問題プリントについて、詳しく解説をしていきます。
1-①の解説と解答
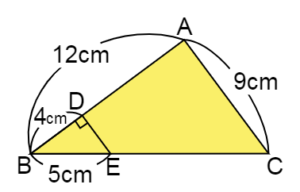
下の図形について、辺DEの長さは何cmか求める問題です。
対応する辺の長さを求める問題は、
ことを利用して求めましょう。
つまり、
対応する辺の長さがわかっている場所を探して、
何倍の拡大図になっているのか、あるいは何分の1の縮図になっているのかを確認し、
計算して求めよう
ということです。
今回、三角形ABCは三角形DBEを拡大したものです。
対応する辺の長さがわかっている場所を探すと、辺ABと辺DBが見つかりますね。
\(12\) cm と \(4\) cmなので、三角形ABCは三角形DBEの \(3\) 倍の拡大図だとわかります。
ということは、辺DEは辺ACを3分の1すれば求められますね。
9 \div 3 =3
\end{eqnarray}
なので、答えは
\(3 \)cm
となります。
1-②の解説と解答
下の図形について、角Aの大きさはいくつか求める問題ですね。

対応する角の大きさを求める問題は、
ことを利用して求めましょう。
つまり、対応する角を見つけるだけでOKです。
同じ位置関係の角を探すと、角Dが見つかりますね。
よって答えは
\(90 \)°
となります。
1-③の解説と解答
下の図形について、ECの長さは何cmか求める問題です。

ECは三角形の辺ではありませんね。
でも良く見ると、辺BCから辺BEの長さを引けば、ECの長さを求められそうです。
①で確認した通り、三角形ABCは三角形DBEの \(3\) 倍の拡大図です。
よって、辺BCの長さは
5 \times 3 =15
\end{eqnarray}
となり、\(15\) cmとわかります。
後は辺BEの長さを引きましょう。
15-5 =10
\end{eqnarray}
よって、答えは
\(10 \)cm
となります。
2の解説と解答
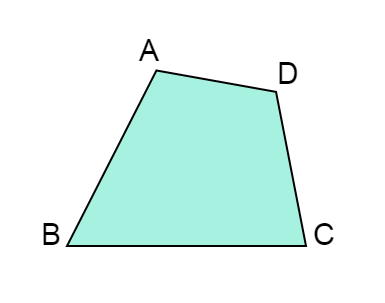
下の図で、頂点Aを中心にして、四角形ABCDの \(1.5\) 倍の拡大図と、\(\dfrac{1}{2}\) の縮図をかく問題です。
拡大図や縮図は、
というやり方でかきます。
中心からのきょりをはかると
AC=\(4\) cm
AE=\(3.4\) cm
となります。
それぞれ\(1.5\) 倍すると
AC=\(4 \times 1.5 =6\) cm
AE=\(3.4 \times 1.5 =5.1\) cm
それぞれ \(\dfrac{1}{2}\) すると
AC=\(4 \div 2 =2\) cm
AE=\(3.4 \div 2 =1.7\) cm
となります。
それぞれの長さを求められたら、実際にかいていきましょう。
まずは以下のように線を引きます。
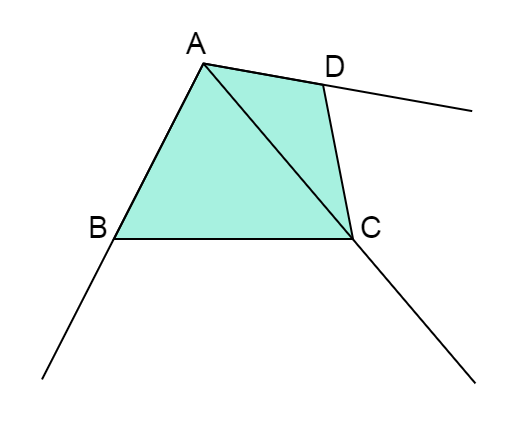
線を引けたら、求めた長さに印をつけて結びましょう。
すると答えは
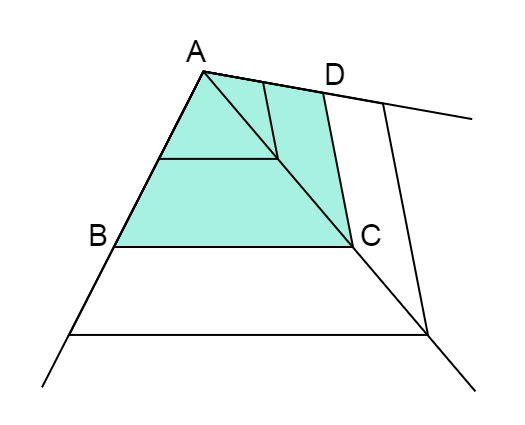
となります。
3の解説と解答
\(2000\) mのきょりは、\(\dfrac{1}{5000}\) の縮図では何cmになるか求める問題です。
\(2000\) mを \(\dfrac{1}{5000}\) の長さにすればよいのですが、答えの単位がcmであることに注意しましょう。
\(2000\) mは \(200000\) cmですね。
後は計算します。
200000 \times \dfrac{1}{5000} = 40 \\
\end{eqnarray}
なので、答えは
\(40\) cm
となります。
4の解説と解答
\(\dfrac{1}{10000}\) の縮図で \(12\) cmの長さは、実際は何kmになるか答える問題です。
すでに \(\dfrac{1}{10000}\) にしてあるものを実際の長さに直すので、\(10000\) 倍すればOKです。
ただし、答える単位がkmなので、単位を直すことに注意しましょう。
では計算します。
12 \times 10000 = 120000 \\
\end{eqnarray}
\(120000\) cm = \(1200\) m = \(1.2\) km
なので、答えは
\(1.2\) km
となります。
5の解説と解答
身長 \(110\) cmのななおさんが街灯(がいとう)から \(4\) m離れたところに立っており、街灯によって \(1\) mのかげができたとき、街灯の高さは何mか求める問題です。
下のような状況ですね。
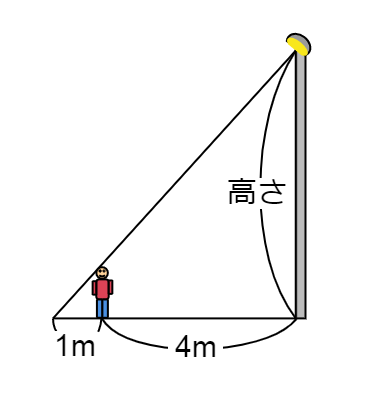
これは、以下のような三角形の関係とみることができます。
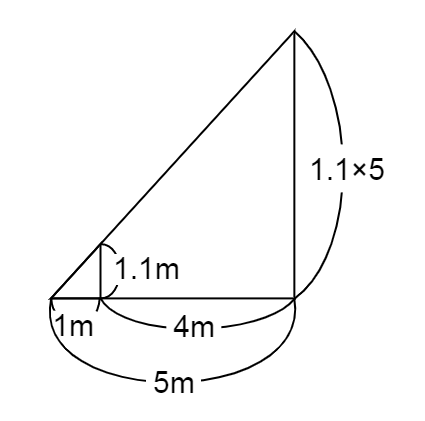
伸長は「m」に直すと\(1.1\) m
かげと街灯から人までのきょりを合わせると \(5\) m ですね。
底辺の関係をみると、小さい三角形の \(5\) 倍が大きな三角形になっていることがわかります。
ということは、街灯の高さは人の高さの \(5\) 倍ということですね。
計算してみましょう。
1.1 \times 5 = 5.5 \\
\end{eqnarray}
よって、答えとなる街灯の高さは
\(5.5\) m
となります。
まとめ
小学6年生 図形の拡大と縮小 問題プリント【まとめテスト】はいかがでしたか?
図形の拡大と縮小の単元をマスターするために、
ようにしましょう。
理解した後はくり返し練習し、図形の拡大と縮小を得意分野にしてくださいね!
※得意を増やす意味⇒得意を伸ばすか、苦手を克服するかどっちがいい?どちらを優先?
その他の問題に取り組みたい方は⇒『小学生 算数プリント一覧』へ



