「小学5年生 比例の問題プリント【まとめテスト】」の解答と解説です。
(↑クリックすると問題に戻ります)」
解説と解答|比例の問題プリント【まとめテスト】
1-①の解説と解答
1個 60円 のりんごがあって、りんごの個数と代金の関係についての表を完成させるという問題です。
1個の場合は、問題にある通り60円ですね。
それが2個ならば2倍、3個ならば3倍となります。
よって、答えは下のような表になります。
| 個数(個) | 1 | 2 | 3 | 4 | 5 | … |
| 代金(円) | 60 | 120 | 180 | 240 | 300 | … |
1-②の解説と解答
りんごの個数が 2倍、3倍…になると、代金はどうなるか答える問題です。
実際に確認してみると、
1個から2個へと2倍になったとき、60円から120円へと2倍になっています。
1個から3個へと3倍になったとき、60円から180円へと3倍になっています。
それ以降も同じ関係が続きます。
よって答えは 2倍、3倍、…となる となります。
1-③の解説と解答
りんごの代金は、りんごの個数に比例するか答える問題です。
②の問題で、りんごの個数が2倍、3倍、…となったときに、代金も2倍、3倍、…となることを確認しました。
よって答えは 比例する となります。
1-④の解説と解答
このりんごを 4個 買うときの、代金を求める式を答える問題です。
「ことばの式」で考えると、
となります。
ここに問題からわかる数をあてはめましょう。
問題からは、
ということがわかりますね。
よって、答えは \(60 \times 4 \) となります。
1-⑤の解説と解答
代金が 480円 になるのは、りんごを何個買ったときか答える問題です。
先ほどの「ことばの式」で考えましょう。
という式ができるので、問題からわかる数をあてはめます。
問題からは、
ということがわかります。
よって、\(60 \times \)個数=\(480 \) となります。
60とかけ算して480になる数は \(480 \div 60 \) で求められます。
よって答えは \(8\)個 となります。
2-①の解説と解答
直方体のたてを 5cm 、横を 6cm と決めて、高さを 1cm、2cm、…と変えたとき、直方体の体積は高さに比例するか答える問題です。
下の図のような状況です。
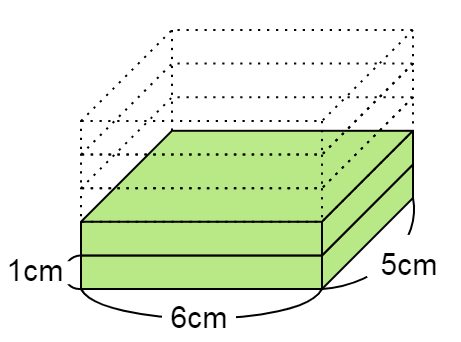
確認しておくと、
でしたね。
実際にどうなるか確認してみましょう。
高さ1cmのときの体積は、\(6 \times 5 \times 1\) で \(30 \) cm3
高さ2cmのときの体積は、\(6 \times 5 \times 2\) で \(60 \) cm3
高さ3cmのときの体積は、\(6 \times 5 \times 3\) で \(90 \) cm3
それ以降も同じ関係が続きます。
ということは、「一方が2倍、3倍、…となったときに、もう片方も2倍、3倍、…となる関係」になっていますね。
よって答えは 比例する です。
2-②の解説と解答
直方体の高さが 2021倍 になると、体積は何倍になるか答える問題です。
比例なので、一方が2倍、3倍、…となったときに、もう片方も2倍、3倍、…となる関係です。
よって、高さが2021倍になれば、体積も2021倍になります。
ということで、答えは 2021倍 となります。
2-③の解説と解答
高さが 21cm のときの、体積を求める式を答える問題です。
「ことばの式」で考えると、
となります。
ここに問題からわかる数をあてはめましょう。
問題からは、
ということがわかります。
よって、答えは \(30 \times 21 \) となります。
2-④の解説と解答
体積が 210cm3 になるのは、高さが何cmのときか答える問題です。
先ほどの「ことばの式」で考えましょう。
という式ができるので、問題からわかる数をあてはめます。
問題からは、
ということがわかりますね。
よって、\(30 \times \)高さ=\(210 \) となります。
30とかけ算して210になる数は \(210 \div 30 \) で求められます。
よって答えは \(7\)cm となります。
まとめ
『小学5年生 比例の問題プリント【まとめテスト】』はいかがでしたか?
比例の問題をマスターするために、
ということを意識して、これからも練習を重ねましょう。
理解した後は繰り返し練習し、比例の問題を得意分野にしてくださいね!
※得意を増やす意味⇒得意を伸ばすか、苦手を克服するかどっちがいい?どちらを優先?
※小学6年生の比例・反比例の問題プリントはこちら
⇒小学6年生 比例と反比例 問題プリント【まとめテスト】
その他の問題に取り組みたい方は⇒『小学生 算数プリント一覧』へ



